Linking expressions and functions
What do we mean by Linking expressions and functions?
There is a subtle but very important shift in Algebraic thinking when we move from thinking of an algebraic expression as a placeholder for a final, numerical answer into thinking about functions. Mathematical Functions, which are at the heart of Mathematics (if they are not the heart itself), are richer but more complicated objects than algebraic expressions, although the two are related and in some contexts are very similar concepts. Differences between algebraic expression as formal symbols and functions become apparent when we use algebra as a Bookkeeping device (see here for an example), where we manipulate these expressions without regard for the actual numerical values that variables -letters- might take. In contrast, a function is all about input/output values, and how these numbers related to each other.
Consider the following excerpt (next three paragraphs) taken from Focus in High School Mathematics: Reasoning and Sense Making, where the authors do a fantastic job in describing what do we mean by Linking expressions and functions:
"Although multiple representations of functions—symbolic, graphical, numerical, and verbal— are commonly seen, the idea of multiple algebraic representations of functions is less commonly made explicit. Different but equivalent ways of writing the same function may reveal different properties of the function.
Symbolic representation shifts to a higher level when we start to use letters to stand for functions and introduce function notation (Saul 2001). The magnitude of this shift is often overlooked. High school students have difficulty with extending the four basic arithmetic operations to functions and also with composition of functions. Embedding these experiences in a context may enhance students’ comprehension of the concepts and improve both their retention and their ability to make connections (Katz 2007),
Building fluency in working with algebraic notation that is grounded in reasoning and sense making will ensure that students can flexibly apply the powerful tools of algebra in a variety of contexts both within and outside mathematics."
I think these last three paragraphs exactly summarize what linking expressions and functions entail and why is it important to make these connections explicitly in the classroom. In fact, they do such a good job, I am going to allow myself to use their example in the following section.
Examples
This next example is entirely due to the authors of Focus in High School Mathematics: Reasoning and Sense Making, and it is reproduced here only for educational purposes. The authors (THE NATIONAL COUNCIL OF TEACHERS OF MATHEMATICS, INC.) are the sole owners of this material. By the way, note that this example also works as an example of Connecting Algebra with Geometry.
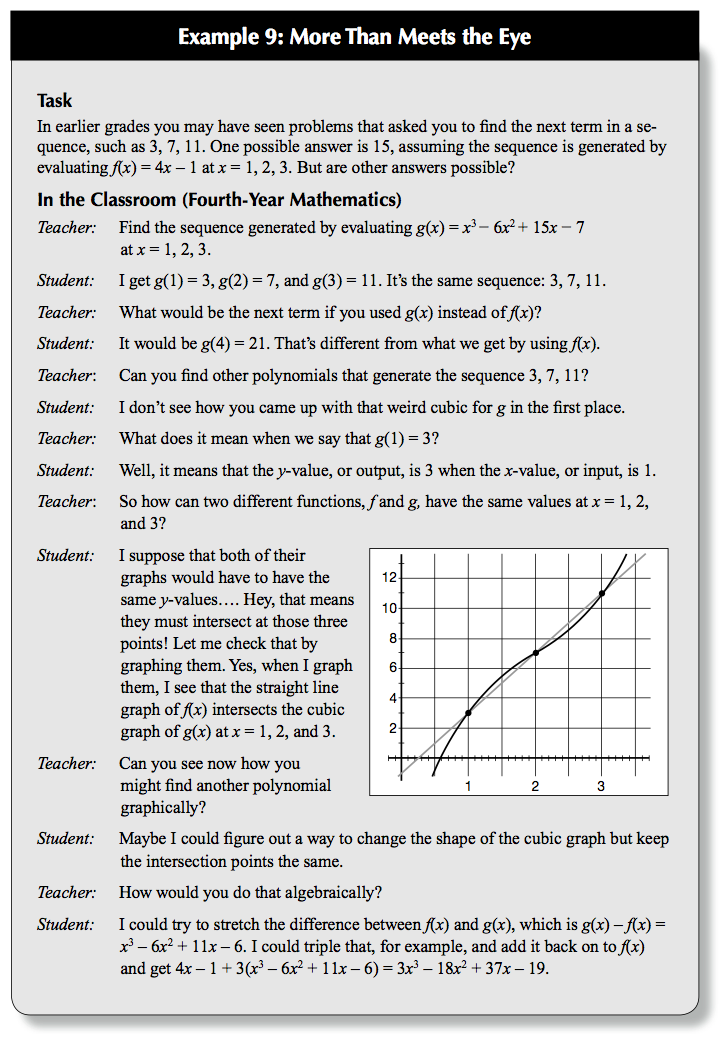
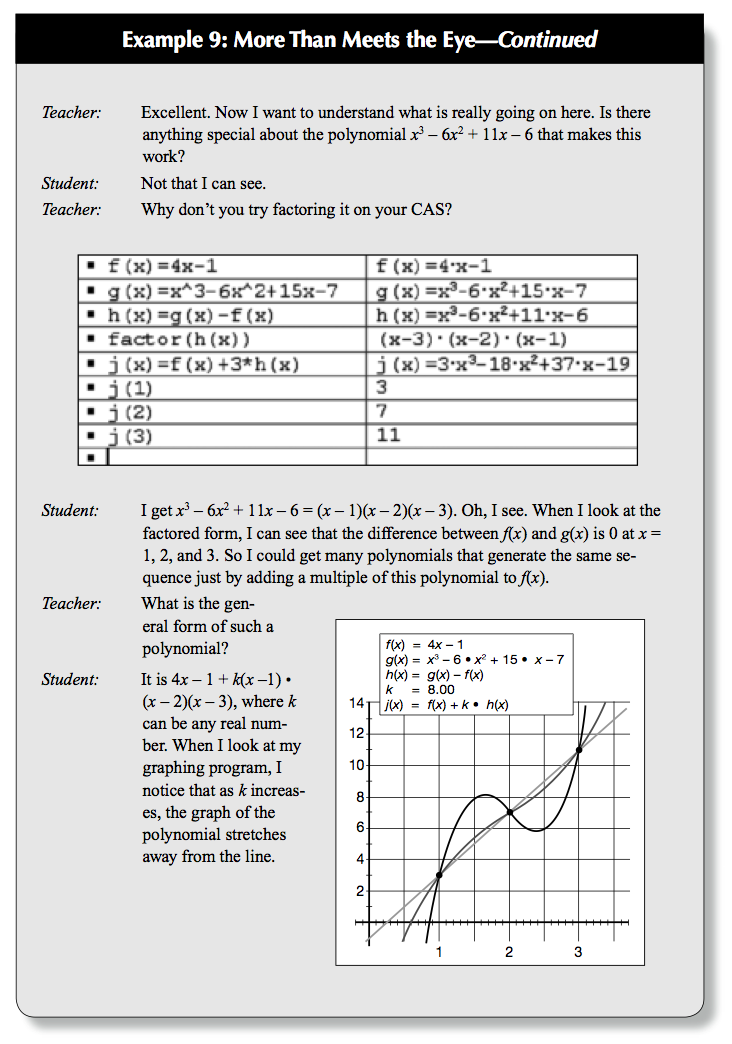
Why Linking expressions and functions is important for the teaching of Algebra in grades 7-12?
Explicit connections between expressions and functions are an essential ingredient of more advance Mathematics, in particularly Calculus. It is in grades 7-12 that proper foundations should be lay so that students have a higher probability of being successful in more advance courses. Moreover, the habit of linking expressions with functions provide students with tools to analyze a problem, identify relevant concepts, representations, or procedures; seek patterns and relationship seeking and using creative and useful connections.
